1. 정보의 표현 단위
컴퓨터는 0과 1, 2진수로만 표현하는 기계이다.
그리고 길이의 단위인 cm, m, km 처럼 컴퓨터가 표현해주는 정보도 단위로 표현할 수 있다.
아래의 표 외에 다른 단위들도 있으면 bit에서 byte로 넘어갈때를 빼고는 보통 \(2^10\)씩 단위가 변한다.
| bit 비트 | 가장 작은 정보 단위로, 0과 1로만 정보를 표현하기 때문에 2가지 정보만 표현할수있다. | |
| byte 바이트 | 8bit | 문자를 표현해주는 가장 작은 단위로, 1bit가 8개 모여서 만들어진다. |
| KB 킬로바이트 | 1024byte | |
| MB 메가바이트 | 1024KB | |
| GB 기가바이트 | 1024MB | |
| WORD 워드 | 8bit, 16bit, 32bit…컴퓨터마다 다름 | 컴퓨터 내부에서 취급되는 정보단위로, 하나의 명령이나 수치가 1word이다. |
위의 표에서 bit는 가장 적은 정보 단위로 0 아니면 1을 표현할 수 있다고 하였는데, 컴퓨터는 1이면 전기신호를 보내고, 0이면 전기신호를 보내지 않는식으로 작동한다.
또한 이를 이용해서 참, 거짓 처럼 두가지 데이터를 표현하는데 유용하다.
2. 컴퓨터에서 양의 정수 표현하기
10진수 9를 2진수로 표현하면 1001이기 때문에 컴퓨터에서 우리가 사용하는 10진수의 한자리 수를 표시하려면 4bit, 메모리 4칸이 필요하다.
그러면 문자를 표현하는 가장 작은 단위인 8bit로는 숫자를 몇까지 표현할 수 있을까?
2진수로 8자리를 계산하면 \(2^8 - 1\)인 255까지 표현할 수 있을것이다.
하지만 C나 Java의 데이터 타입 중 1Byte 크기를 가지는 데이터 타입인 char나 byte를 보면 수의 범위가 -128 ~ 127이다.
나머지 절반은 어디로갔을까?

위의 그림에서 만약 8칸 모두 숫자를 넣어 표현하게 된다면 컴퓨터는 양수만 표현하고, 음수는 표현할 수 없게 될것이다.
그래서 위의 그림에서 제일 앞칸인 \(2^7\) 자리는 일단 비워두고 앞의 7칸에서만 숫자를 표시한다.
그 다음 양수라면 \(2^7\) 자리에는 0이, 음수라면 1이 와서 앞의 7칸에 들어있는 수가 양수인지 음수인지 알수 있게 한다.
그런데, 이렇게 한다면 한가지 문제가 생긴다.
컴퓨터에서 2진수 0000 0001은 1이고, 0000 0000은 0이다.
그러면 1000 0000은 -0일까? -0이라는 숫자가 있기는 할까?
이 문제는 보수를 이용하면 해결할 수 있다.
3. 보수
보수는 어떤수를 만들기 위해 보충해주어야 하는 수를 말한다.
예를들어 7이라는 수가 있고, 10을 만들고 싶다. 그러면 3과 7은 서로 보수관계가 된다.
보수에는 1의 보수와 2의 보수가 있다.
1의 보수는 최댓값을 형성하는데 서로 보완 관계에 있는 두 수를 말한다.
예를들어 10진수의 1의 자리에서 가장 큰 수는 9이다.
이때 4와 5를 더하면 9가 되므로, 4의 보수는 5, 5의 보수는 4이며, 두 수는 1의 보수관계에 있다.
컴퓨터의 2진수에서 예를 들어보면 어떤 숫자를 각 자리의 값이 1인 수와 빼면 된다.
예를들어서 \(0101\)이라는 수가 있고, 이 수를 \(1111\)에서 빼주면 \(1010\)이 된다.
각 자리 수를 0을 1로, 1을 0으로만 바꿔주면 되는것이다.
그리고 2의 보수는 다음 자리수로 넘어가기 위해 서로 보완 관계에 있는 두 수를 말한다.
다시 10진수로 예를 든다면 1의자리에서 2의자리로 넘어가면 만날 수 있는 첫번째 수는 10이다.
4에서 6을 더한다면 10을 만들 수 있으니, 4의 2의 보수는 6, 6의 2의 보수는 4이며, 두 수는 2의 보수관계에 있다.
그러면 2진수로 다시 예를 들면 \(0101\)이라는 수의 2의 보수는 \(1011\)이 되는것이다.
1의 보수와 2의 보수를 살펴보면 2의 보수는 1의보수에서 1을 더한 값과 같다.
그럼 위의 보수 방법을 이용하여 음수를 표현해보자.
4. 컴퓨터에서 음의 정수 표현하기
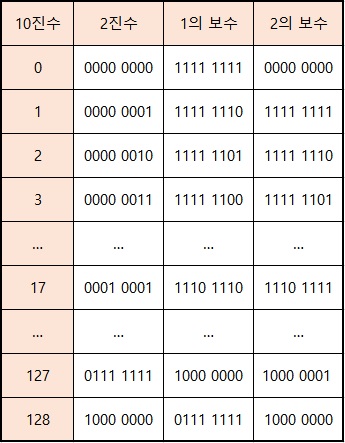
위의 그림을 보면 0의 1의 보수는 1111 1111이다.
아까 걱정하던 -0이 나와버렸으니 1의 보수로 음수를 표현하건 적절하지 않다.
그런데 2의 보수를 보니 0000 0000이므로 이전에 보던 0이 하나만 나온다.
또 양수는 127까지밖에 표현하지 못했지만 음수는 -128 하나를 추가로 표현할 수 있다.
- 참고
컴퓨터는 8bit로 정수를 표현할 때 8자리가 넘어가 9자리가 되어버리면 9번째 자리는 무시하기 때문에 위의 그림에서 0의 2의 보수가 1 0000 0000이 아닌 0000 0000이 된다.)