1. Binary Search
이진탐색, 이분탐색으로 불리며, 탐색해야 하는 부분을 반으로 나누어 찾는 방식이다.
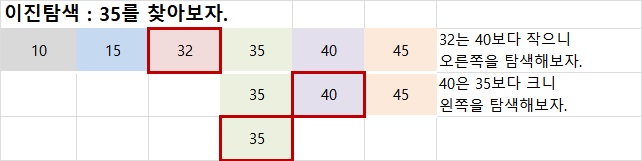
배열에 있는 숫자 중 35가 몇번째에 있는지 알고 싶다면 일단 배열을 반으로 나누어 가운데 숫자를 본다.
가운데에 있는 숫자가 35보다 크다면 35는 배열의 앞 절반에, 가운데 숫자가 35보다 작다면 배열의 뒤 절반에 있을것이다.
이렇게 반으로, 반으로 나누다 보면 내가 찾는 숫자가 나올수도, 혹은 범위가 최소(1개)가 되어 숫자가 나오지 않을 수도 있다.
일정 범위의 숫자를 반씩 나눠서 범위를 좁혀가는것이 마치 병뚜껑 숫자 맞추기와 비슷하다.
대신 이진 탐색에서 주의할 점은 배열의 내용이 정렬되어 있어야 한다는 것이다.
참고 : 하버드 CS50강의
1-1. 시간복잡도
이진탐색은 반씩 나눠서 진행된다.
예를들어 배열의 길이가 8이면, \(8/2\), \((8/2)/2\), \(((8/2)/2)/2\) 의 인덱스 위치를 탐색하고, 3번만에 원하는 값이 있는지 확인할 수 있다.
그래서 시간복잡도는 $O(log n)$가 된다.
2. 구현하기
아래의 이진탐색은 배열이 정렬되어 있다는 가정 하에 만들었다.
반복문에서 조건을 start <= end로 잡은 것은 start == end가 되는 시점은 탐색해야 할 부분이 한개밖에 안남았을 때, 즉 마지막 방인 경우이기 때문이다.
start > end가 되면 더이상 탐색할 배열이 남아있지 않다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# 값의 위치를 반환
def binarySearch(data, search) :
start = 0 # 시작 인덱스
end = len(data) - 1 # 마지막 인덱스
while start <= end :
mid = (start + end) // 2 # 중간 인덱스
# 만약 중간이 찾는값과 같다면 중간인덱스 반환
if data[mid] == search :
return mid
# 중간값이 찾는값보다 크다면 왼쪽 탐색
elif data[mid] > search :
end = mid - 1
# 중간값이 찾는값보다 작다면 오른쪽 탐색
elif data[mid] < search :
start = mid + 1
return False